介绍

本文将描述如何实现一个推箱子 📦, 示例代码使用 Rust 语言 🦀 编写.

推箱子的起源

推箱子在 1981 年由日本人今林宏行(いまばやしひろゆき)所创造, 第一个版本于 1982 年 12 月发行, 名为仓库番, 字面意思为 "仓库管理员" 👷.¹ 英文名为: Sokoban 或 Soukoban.

截至 2024 年, 最新版本推箱子(みんなの倉庫番)于 2019 年 8 月在 PlayStation 4 平台发行.¹

最新版本的推箱子在角色控制方面相较于其最初的版本并未见明显改进, 本文后续将介绍一种纯鼠标控制的角色控制方法 🖱️.

为什么通过案例来讲解

本文以推箱子为案例, 深入浅出的描述软件开发过程. 通过案例讲解有以下目的:

结合实例的学习可以将知识和应用结合在一起, 使读者无需被 "学这个有什么用?" 所困扰 🤔.
提供丰富的实例. 推箱子问题本身还附带了许多子问题, 很适合作为例子使用.
众多读者对游戏有浓厚的兴趣 🎮.

为什么选择推箱子作为案例

之所以选择推箱子, 是因为它具有以下特点:

规则简单: 可以专注于实现功能, 而非理解复杂的游戏规则和机制.
基本功能易于实现: 如推箱子和通关判断.
有具有挑战的高级功能: 如纯鼠标控制, 逆推等.
有需要深入钻研的求解器: 用于自动求解推箱子关卡.

推箱子的实现既可以简单也可以复杂, 读者可以根据自身的情况选择学习的深度.

需要具备的知识

具备 Rust 语言的语法基础, 或熟悉一门命令式编程语言.
有关高级功能和求解器的章节: 具备数据结构与算法的基础知识, 如 A* 搜索算法的工作原理.

内容范围

本文将描述基本功能的具体实现方法, 高级功能的实现方法以及求解器的实现思路.
但本文不涉及以下内容:

Rust 语言本身: 本文中出现的算法适用于其他编程语言, 但依然会涉及部分 Rust 相关内容的讲解, 如错误处理 (Rust 在这方面和其他语言不太一样), 不感兴趣的读者可以直接跳过这部分内容.
游戏引擎: 本文中的推箱子实现并不依赖游戏引擎, 比如有的推箱子实现需要用到射线检测.
其他推箱子变体².

项目代码

完整的项目代码位于:

ShenMian/soukoban: 推箱子相关算法实现.
ShenMian/sokoban-rs: 基于 Bevy 引擎的推箱子实现.

拓展资料

推荐视频 🎥:

【GM】火遍全球的推箱子，那些你所不知道的故事！· Bilibili: 该视频详细介绍了推箱子的历史和发展.

版权

本文遵循 CC-BY 4.0 协议发布. 部分图片来源于互联网, 版权归原作者所有.

https://www.sokoban.jp/history.html

https://en.wikipedia.org/wiki/Sokoban#Variants

设计

结构体设计

Map: 存储地图数据.
- 包含所有地图元素的数组.
- 包含玩家位置, 箱子和目标位置: 方便快速读取, 否则需要遍历数组来获取相应元素的坐标.
Actions: 存储玩家的动作, 包括动作的类型(移动或推动), 以及方向(上下左右).
Level: 关卡, 包含地图和玩家动作. 可以执行或撤销动作.

将 Level 中与地图相关的内容分离到 Map 中, 是为了将地图数据与关卡功能分离. 许多涉及地图的操作(例如计算两个地图之间的相似度)与关卡功能无关.

Map 的数组是否应该包含玩家和箱子元素? 🤔

包含:

在修改玩家位置或移动箱子时, 需要同步数组中的数据. 可能引入导致数据不一致的 BUG. 但因为实现十分简单, 因此引入 BUG 的可能性不大.

存在数据冗余, 但是冗余的数据量很小, 不至于造成显著的内存占用率变化.

不包含: 读取时需要判断是否与玩家或任意箱子的位置相同, 如果有就追加相关元素的枚举值. 导致读取比写入有更大的开销. 取比写入开销大违反直觉, 违背了 POLA¹.

综上所述, 本文倾向于在数组里包含这些元素.

Map 的数组应该是一维的还是二维的? 🤔

由于该数组是动态数组, 二维动态数组的分配与释放需要更大的开销. 而使用一维动态数组, 内存布局会更加紧凑, 且可以提供使用二维坐标读取地图内容的关联函数. 因此使用一维数组更为合适.

转换关系

flowchart LR
    A[String] -->|XSB 格式| B[Map]
    A -->|LURD 格式| C[Actions]
    C -->|重建| B
    B --> D[Level]

https://en.wikipedia.org/wiki/Principle_of_least_astonishment

关卡

XSB 格式

推箱子关卡所使用的 XSB 格式因其简洁和直观而受到了广泛的认可和应用, 最初由 XSokoban 所使用. 该格式使用 ASCII 字符来表示地图元素, 并支持注释和附加元数据.
以关卡 Boxworld #1 为例:

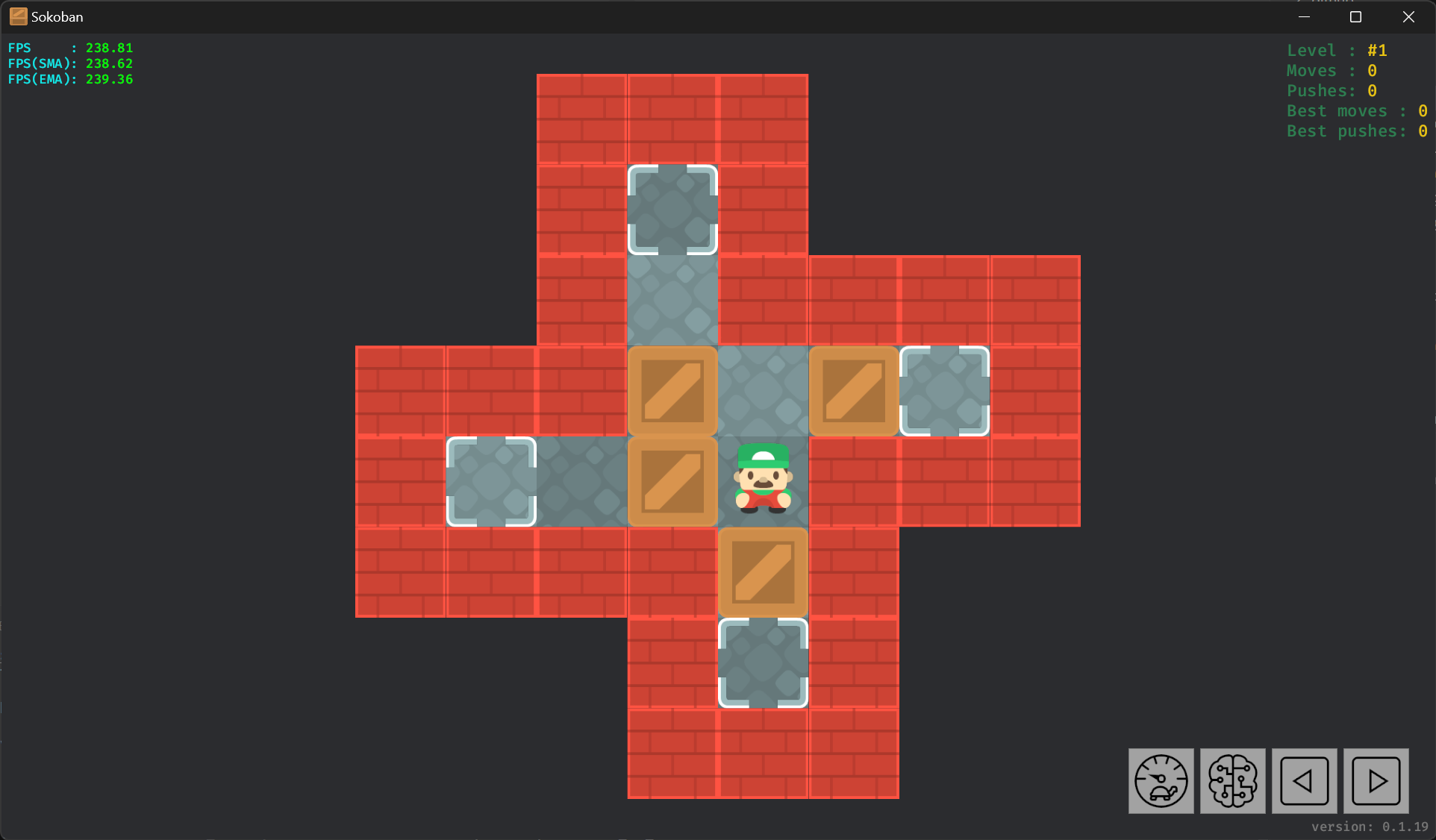
Boxworld #1

其 XSB 格式关卡的数据如下:

;Level 1
__###___
__#.#___
__#-####
###$-$.#
#.-$@###
####$#__
___#.#__
___###__
Title: Boxworld 1
Author: Thinking Rabbit

上面的关卡数据大致可分为以下几种:

第 1 行, 单行注释, 以 ; 开头.
第 2-9 行, 地图数据, 使用 ASCII 字符表示.
第 10-11 行, 元数据, 包括关卡标题和作者的信息.

地图数据

ASCII 符号	描述
`<SPACE>`/`-`/`_`	地板
`#`	墙体 🧱
`$`	箱子 📦
`.`	目标 🎯
`@`	玩家 👷
`+`	位于目标上的玩家
`*`	位于目标上的箱子

其中地板一共使用了三种符号表示, 是因为连续的空格在某些在线论坛或邮件中可能被截断, 因此使用连字符(-)和下划线(_)来替代¹.

元数据

第 10 行的 Title: Boxworld 1 可以解释为键为 title (不区分大小写), 值为 Boxworld 1 的元数据.
还有一种用于多行注释的特殊元数据. 内容通过 comment: 和 comment-end: 包裹. 这也是唯一支持值有多行的元数据.

!!! info 多行注释还存在一种以 comment: 和 comment_end: 包裹的写法, 与之前提到的多行注释不同，这种多行注释使用下划线(_)来替代连字符(-)分割单词.
本文将这种格式视为无效格式, 其可能是在批量替换 _ 和 - 字符时意外产生的.

游程编码 🗜️

游程编码(Run-length encoding, RLE)是无损数据压缩的一种形式, 常被应用于推箱子关卡和解决方案的压缩.

###
#.###
#*$ #
# @ #
#####

经 RLE 编码后可得:

3#
#.3#
#*$-#
#--@#
5#

可以看出, 虽然编码后的关卡有更小的体积, 但不再能直观地看出关卡的结构.

RLE 编码后的关卡通常还会使用 | 来分割行, 而非 \n. 使其看上去更加紧凑:

3#|#.3#|#*$-#|#--@#|5#

只需要对原本的语句进行修改即可提供对 | 分割行的支持:

for line in str.lines() { ... SKIP ... }

for line in str.split(['\n', '|']) { ... SKIP ... }

解码

下面是一个 RLE 解码函数的实现:

pub fn rle_decode(str: &str) -> Result<String, DecodeRleError> {
    let mut result = String::new();

    let mut length_string = String::new();
    let mut iter = str.chars();
    while let Some(char) = iter.next() {
        if char.is_ascii_digit() {
            length_string.push(char);
            continue;
        }
        let mut token = String::new();
        if char == '(' {
            let mut nesting_level = 0;
            for char in &mut iter {
                if char == '(' {
                    nesting_level += 1;
                } else if char == ')' {
                    if nesting_level == 0 {
                        break;
                    }
                    nesting_level -= 1;
                }
                token.push(char);
            }
        } else {
            token = char.to_string();
        }
        let length = length_string.parse().unwrap_or(1);
        result += &token.repeat(length);
        length_string.clear();
    }
    if !length_string.is_empty() {
        return Err(DecodeRleError::EndWithDigits(
            length_string.parse().unwrap(),
        ));
    }
    if result.contains('(') {
        return rle_decode(&result);
    }
    Ok(result)
}

其他格式

MF8

中文论坛魔方吧²使用 MF8 格式:

[soko=8,8]
__HHH___
__H.H___
__H_HHHH
HHH$_$.H
H._$aHHH
HHHH$H__
___H.H__
___HHH__
[/soko]

特殊关卡

玩家不可达区域存在箱子

Sasquatch #41 by David W. Skinner

   #####
   #   #
 ###   ########
##  ***    # # #
 #  * *    ## # #####
##  ***   ## # ##   ##
 ###   #### # # #   #
   #   # # # ####$ $###
  ##   ## # ##  $...$ ##
   ##### # ##    .@.  #
        # # #   $...$ ##
         ########$ $###
                #   #
                #####

存在只有空元素的行

"Steaming Hot" by David Buchweitz

  #      #
 #   #  #
  # #  #
   # #  #
  #   #  #
 #   #  #
  # #  #
-
##########
#........####
# $$$$$$$#  #
#.$......#  #
# $$$$$$ #  #
#......$+#  #
#$$$$$$$ #  #
#        ####
##########

无完整外墙

部分推箱子程序支持无完整外墙的关卡.
在本文中, 这种关卡属于无效关卡. 但可以通过为其添加外墙的方式来转换为有效关卡.

"No walls" by Rincewind

* ** *
  **
**@$.*
  **
* ** *

拓展资料

https://en.wikipedia.org/wiki/Run-length_encoding.

参考

http://sokobano.de/wiki/index.php?title=Level_format.

http://sokobano.de/wiki/index.php?title=Level_format

http://www.mf8-china.com/forum.php

表示

表示地图 🗺️

元素的表示

地图共包含 5 种元素, 这些元素可能在一个格子内叠加(比如玩家位于目标上).
最小的数据存储单元字节包含 8 个比特, 足以表示 5 种元素. 因此可以使用一个字节的空间来存储单个地图格子, 其中的每个比特表示一种地图元素.
创建用于表示地图元素的标志位(bit flags):

use bitflags::bitflags;

bitflags! {
    pub struct Tiles: u8 {
        const Floor = 1 << 0;
        const Wall = 1 << 1;
        const Box = 1 << 2;
        const Goal = 1 << 3;
        const Player = 1 << 4;
    }
}

这样可以很方便的表示多种地图元素叠加的情况, 如使用 Tiles::Floor | Tiles::Goal | Tiles::Player 来表示玩家位于目标上, 而目标位于地板上的情况.
利用比特位表示元素不仅使得判断元素是否存在、添加或移除某个元素等操作变得非常便捷, 而且还有位运算带来的性能上的优势.

地图的存储

使用一维数组来存储地图数据, 使用二维向量(数学)存储地图尺寸.

use nalgebra::Vector2;

pub struct Map {
    data: Vec<Tiles>,
    dimensions: Vector2<i32>,
    // ... SKIP ...
}

这样设计有以下考量:

与拥有固定尺寸棋盘的棋类游戏不同, 推箱子关卡的尺寸是可变的, 因此使用动态数组.
使用一维数组而非二维数组 (Vec<Vec<Tiles>>) 是因为一维数组更平坦(flatten), 能确保动态数组的元素在内存中是紧密排列的, 根据数据局部性原理, 这通常能提高内存读取效率. 此外, 由于结构更为简单, 使得部分操作的代码更为简洁高效, 比如调整地图尺寸.

但这也意味着通过二维坐标访问地图元素需要手动计算一维数组中对应的下标, 可以通过以下方式实现:

impl Index<Vector2<i32>> for Map {
    type Output = Tiles;

    fn index(&self, position: Vector2<i32>) -> &Tiles {
        assert!(0 <= position.x && position.x < self.dimensions.x && 0 <= position.y);
        &self.data[(position.y * self.dimensions.x + position.x) as usize]
    }
}

impl IndexMut<Vector2<i32>> for Map {
    fn index_mut(&mut self, position: Vector2<i32>) -> &mut Tiles {
        assert!(0 <= position.x && position.x < self.dimensions.x && 0 <= position.y);
        &mut self.data[(position.y * self.dimensions.x + position.x) as usize]
    }
}

这样便可以直接通过二维坐标访问地图元素, 例如访问地图 $(1, 1)$ 位置的元素: map[Vector2::new(1, 1)].
这样的设计不仅可以享受了二维数组访问方式的便捷性, 还能保留了一维数组带来的性能优势.

值得注意的是其中的断言, 该函数最终通过下标访问一维数组由 Index<> for Vec<> 进行了部分越界检查, 但越界检查依然不完整, 没有涵盖以下无效情况:

坐标 x 可以超出地图宽度的情况, 但其一维数组下标依然有效.
坐标 x, y 中存在负数, 但其一维数组下标依然可能是正数.

表示关卡

关卡数据可分为三个部分: 地图数据, 元数据和注释. 其中注释可以作为元数据.
元数据是一个键值对的集合, 且键不重复, 因此可以使用 HashMap 容器来存储. 可以使用下面的结构体存储关卡数据:

use std::collections::HashMap;

pub struct Level {
    map: Map,
    metadata: HashMap<String, String>,
    // ... SKIP ...
}

将地图从关卡中拆分是因为地图涉及大量的关联函数, 如果都放在 Level 里会导致其变得过于庞大.
为了提升代码的可读性和可维护性, 将相关代码拆分到 Map 中, 并通过实现 Deref trait, 使得用户能够透明地引用到 Level 内部的 Map.

构造 🏗️

从 XSB 格式字符串构造关卡

关卡解析可以分为两部分: 地图解析, 元数据和注释解析.

一个 XSB 格式的关卡文件中通常包含多个关卡, 不同关卡之间通过空行分割. 因此解析 XSB 格式的数据大致可分为两个步骤:

多个关卡之间的分割.
单个关卡的解析.

flowchart LR
    A[包含多个关卡的字符串] -->|Level::to_group| B
    B[包含单个关卡的字符串] --> C{是否经过\n RLE 压缩?}
    C -->|是| D[RLE 压缩字符串]
    C -->|否| E
    D -->|rle_decode| E
    E[XSB 字符串]

多个关卡之间的分割

定义关联函数 Level::to_groups, 接受包含多个关卡的字符串, 返回包含单个关卡的字符串切片的迭代器.

impl Level {
    // ... SKIP ...

    fn to_groups(str: &str) -> impl Iterator<Item = &str> + '_ {
        str.split(['\n', '|']).filter_map({
            let mut offset = 0;
            let mut len = 0;
            let mut in_block_comment = false;
            let mut has_map_data = false;
            move |line| {
                len += line.len() + 1;

                let trimmed_line = line.trim();
                if !in_block_comment && (trimmed_line.is_empty() || offset + len == str.len() + 1) {
                    let group = &str[offset..offset + len - 1];
                    offset += len;
                    len = 0;
                    if group.is_empty() || !has_map_data {
                        return None;
                    }
                    has_map_data = false;
                    Some(group)
                } else {
                    if in_block_comment {
                        if trimmed_line.to_lowercase().starts_with("comment-end") {
                            // Exit block comment
                            in_block_comment = false;
                        }
                        return None;
                    }
                    if let Some(value) = trimmed_line.to_lowercase().strip_prefix("comment:") {
                        if value.trim_start().is_empty() {
                            // Enter block comment
                            in_block_comment = true;
                        }
                        return None;
                    }
                    if has_map_data || !is_xsb_string(trimmed_line) {
                        return None;
                    }

                    has_map_data = true;

                    None
                }
            }
        })
    }
}

出于性能方面的考虑, 解析关卡数据时应该减少不必要的动态内存分配:

由于函数 Level::to_groups 仅对输入字符串进行解析, 不涉及修改操作, 因此其参数类型为字符串切片 &str, 类似 C++ 中的 std::string_view.
单个关卡的数据是连续的, 因此可以使用字符串切片来表示, 无需再使用 String 来存储地图数据.

以上方法通过直接引用原始字符串避免了内存分配, 减少内存占用的同时提高了执行效率. 而且还使得对内存的访问更加局部化.

返回迭代器是因为可以利用迭代器的惰性求值, 来惰性的分割关卡.

这种实现方式有以下优点:

支持流式读取并构造关卡. 例如, 通过利用 BufReader¹ 支持从大文件中逐步地加载关卡数据, 避免了内存的大量占用和性能瓶颈.
读取第 n 个关卡. 跳过前 n-1 个关卡, 只对第 n 个关卡的数据进行解析. 可以加快从多个关卡中加载单个关卡的速度.

impl Level {
    pub fn load(str: &str) -> impl Iterator<Item = Result<Self, ParseLevelError>> + '_ {
        Self::to_groups(str).map(Self::from_str)
    }

    pub fn load_nth(str: &str, id: usize) -> Result<Self, ParseLevelError> {
        let group = Self::to_groups(str).nth(id - 1).unwrap();
        Self::from_str(group)
    }
    
    // ... SKIP ...
}

这样便实现的关卡的惰性解析. 比如搜索完全一致的关卡:

let str = "..."; // 海量关卡
for level in Level::load(&fs::read_to_string(path).unwrap()).filter_map(|x| x.ok()) {
    // ... SKIP ...
}

若循环体在循环的过程中通过 break 语句提前退出循环, 未被循环到的关卡将不会被解析, 从而减少不必要的计算.

值得注意的是, 虽然在一些编程语言中 Level::load_nth 的实现是多余的, 但在 Rust 中, 迭代器先 map 后 nth 与先 nth 后 map 并不等价, 前者会执行 n 次 map, 而后者只会执行一次 map, 显著提高了效率.

单个关卡的解析

解析元数据和注释

定义一个关联函数 Level::from_str, 作为 Level 的构造函数. 该函数只负责解析关卡的元数据和注释, 地图数据的进一步解析则由 Map::from_str 负责:

impl Level {
    pub fn from_str(str: &str) -> Result<Self, ParseLevelError> {
        // ... SKIP ...
        Ok(Self {
            map: Map::from_str(/* ... SKIP ... */)?,
            metadata,
            // ... SKIP ...
        })
    }
    // ... SKIP ...
}

关联函数 Level::from_str 需要将元数据存储到 HashMap 容器中, 同时提取地图数据后续交给 Map::from_str 做进一步解析.
由于地图数据是连续的, 所以也可以使用字符串切片表示.

impl Level {
    pub fn from_str(str: &str) -> Result<Self, ParseLevelError> {
        let mut map_offset = 0;
        let mut map_len = 0;
        let mut metadata = HashMap::new();
        let mut comments = String::new();
        let mut in_block_comment = false;
        for line in str.split_inclusive(['\n', '|']) {
            if map_len == 0 {
                map_offset += line.len();
            }

            let trimmed_line = line.trim();
            if trimmed_line.is_empty() {
                continue;
            }

            // Parse comments
            if in_block_comment {
                if trimmed_line.to_lowercase().starts_with("comment-end") {
                    // Exit block comment
                    in_block_comment = false;
                    continue;
                }
                comments += trimmed_line;
                comments.push('\n');
                continue;
            }
            if let Some(comment) = trimmed_line.strip_prefix(';') {
                comments += comment.trim_start();
                comments.push('\n');
                continue;
            }

            // Parse metadata
            if let Some((key, value)) = trimmed_line.split_once(':') {
                let key = key.trim().to_lowercase();
                let value = value.trim();

                if key == "comment" {
                    if value.is_empty() {
                        // Enter block comment
                        in_block_comment = true;
                    } else {
                        comments += value;
                        comments.push('\n');
                    }
                    continue;
                }

                if metadata.insert(key.clone(), value.to_string()).is_some() {
                    return Err(ParseLevelError::DuplicateMetadata(key));
                }
                continue;
            }

            // Discard line that are not map data (with RLE)
            if !is_xsb_string(trimmed_line) {
                if map_len != 0 {
                    return Err(ParseMapError::InvalidCharacter(
                        trimmed_line
                            .chars()
                            .find(|&c| !is_xsb_symbol_with_rle(c))
                            .unwrap(),
                    )
                    .into());
                }
                continue;
            }

            if map_len == 0 {
                map_offset -= line.len();
            }
            map_len += line.len();
        }
        if !comments.is_empty() {
            debug_assert!(!metadata.contains_key("comments"));
            metadata.insert("comments".to_string(), comments);
        }
        if in_block_comment {
            return Err(ParseLevelError::UnterminatedBlockComment);
        }
        if map_len == 0 {
            return Err(ParseLevelError::NoMap);
        }

        Ok(Self {
            map: Map::from_str(&str[map_offset..map_offset + map_len])?,
            metadata,
            // ... SKIP ...
        })
    }
    // ... SKIP ...
}

在处理过程中, 注释内容被特别识别, 并作为键为 comments 的元数据, 一同存储到 Level::metadata 中.

解析地图数据

解析地图数据可以分为以下几个部分:

去除多余空白: 首先, 移除每行右侧的空白字符. 随后, 确定地图左侧的最小缩进量(即每行左侧空白字符的最小数量), 并据此剔除左侧的多余空白.
确定地图尺寸: 与 MF8 格式不同, XSB 格式并不直接附带地图尺寸数据, 因此需要通过解析关卡地图数据来确定地图尺寸.
RLE 解码: 如果地图数据经过 RLE 编码, 进行解码操作.
解析地图数据: 地图数据使用 Tiles 表示, 写入缓冲区中.
填充地板: 使用洪水填充算法从玩家位置开始, 以墙为边界填充地板.

impl Map {
    pub fn from_str(str: &str) -> Result<Self, ParseMapError> {
        debug_assert!(!str.trim().is_empty(), "string is empty");

        // Calculate map dimensions and indentation
        let mut indent = i32::MAX;
        let mut dimensions = Vector2::<i32>::zeros();
        let mut buffer = String::with_capacity(str.len());
        for line in str.split(['\n', '|']) {
            let mut line = line.trim_end().to_string();
            if line.is_empty() {
                continue;
            }
            // If the `line` contains digits, perform RLE decoding
            if line.chars().any(char::is_numeric) {
                line = rle_decode(&line).unwrap();
            }
            dimensions.x = dimensions.x.max(line.len() as i32);
            dimensions.y += 1;
            indent = indent.min(line.chars().take_while(char::is_ascii_whitespace).count() as i32);
            buffer += &(line + "\n");
        }
        dimensions.x -= indent;

        let mut instance = Map::with_dimensions(dimensions);

        // Parse map data
        let mut player_position: Option<Vector2<_>> = None;
        for (y, line) in buffer.lines().enumerate() {
            // Trim map indentation
            let line = &line[indent as usize..];
            for (x, char) in line.chars().enumerate() {
                let position = Vector2::new(x as i32, y as i32);
                instance[position] = match char {
                    ' ' | '-' | '_' => Tiles::empty(),
                    '#' => Tiles::Wall,
                    '$' => {
                        instance.box_positions.insert(position);
                        Tiles::Box
                    }
                    '.' => {
                        instance.goal_positions.insert(position);
                        Tiles::Goal
                    }
                    '@' => {
                        if player_position.is_some() {
                            return Err(ParseMapError::MoreThanOnePlayer);
                        }
                        player_position = Some(position);
                        Tiles::Player
                    }
                    '*' => {
                        instance.box_positions.insert(position);
                        instance.goal_positions.insert(position);
                        Tiles::Box | Tiles::Goal
                    }
                    '+' => {
                        if player_position.is_some() {
                            return Err(ParseMapError::MoreThanOnePlayer);
                        }
                        player_position = Some(position);
                        instance.goal_positions.insert(position);
                        Tiles::Player | Tiles::Goal
                    }
                    _ => return Err(ParseMapError::InvalidCharacter(char)),
                };
            }
        }
        if instance.box_positions.len() != instance.goal_positions.len() {
            return Err(ParseMapError::BoxGoalMismatch);
        }
        if instance.box_positions.is_empty() {
            return Err(ParseMapError::NoBoxOrGoal);
        }
        if let Some(player_position) = player_position {
            instance.player_position = player_position;
        } else {
            return Err(ParseMapError::NoPlayer);
        }

        instance.add_floors(instance.player_position);

        Ok(instance)
    }
    // ... SKIP ...
}

其中部分验证解决方案步骤能发现的错误也可以在模拟玩家移动的步骤中提前发现, 但为了保持代码的简洁, 这里不做检查.

性能测试

项目	平均耗时
加载 3371 个关卡	23.714 ms
加载第 3371 个关卡	3.2700 ms

根据数据, 可以得出以下结论:

加载单个关卡的平均耗时约 7 μs.
加载 n 个关卡和加载第 n 个关卡的耗时存在显著差异, 说明后者确实有性能的提升.

错误处理

在解析地图数据的过程中, 应该关注可能发生的错误, 并进行相应的检查.
幸运的是, 许多常见的错误都可以在解析数据的同时顺便进行排查, 这样只会带来极小的额外开销, 从而确保地图的正确性和完整性.

#[derive(Error, Clone, Eq, PartialEq, Debug)]
pub enum ParseLevelError {
    // ... SKIP ...
}

#[derive(Error, Clone, Eq, PartialEq, Debug)]
pub enum ParseMapError {
    // ... SKIP ...
}

impl From<ParseMapError> for ParseLevelError {
    fn from(error: ParseMapError) -> Self {
        ParseLevelError::ParseMapError(error)
    }
}

重载 ParseMapError 到 ParseLevelError 的转换, 以便 Level::from_str 直接返回 Map::from_str 中的错误.
遵循 Rust API Guidelines (C-GOOD-ERR)² 的建议, 应该为错误类型实现 Debug / Error 和 Display 等 trait. 本文使用库 thiserror³ 来自动完成这一步骤.

从解决方案构造关卡

从解决方案构造关卡可以分为以下几个部分:

确定地图尺寸: 地图的尺寸等于玩家移动范围加上 1, 以包含外墙.
模拟玩家移动: 模拟玩家的移动, 并记录三组数据, 分别是: 当前箱子位置和箱子初始位置.

玩家只能在地板上移动, 因此将玩家移动到的位置设为地板. 若玩家推动了箱子, 且该箱子移动前的位置不再当前箱子位置中, 添加到箱子位置中. 箱子当前位置在模拟结束后, 当前箱子位置即最终箱子位置. 若解决方案正确, 那么最终箱子位置与目标位置相同.
添加墙壁: 在地板周围添加墙壁, 以形成完整的关卡结构.
验证解决方案: 在构造的关卡里验证解决方案的有效性. 若验证失败, 则表示解决方案不正确.

impl Map {
    pub fn from_actions(actions: &Actions) -> Result<Self, ParseMapError> {
        let mut min_position = Vector2::<i32>::zeros();
        let mut max_position = Vector2::<i32>::zeros();

        // Calculate the dimensions of the player's movement range
        let mut player_position = Vector2::zeros();
        for action in &**actions {
            player_position += &action.direction().into();
            min_position = min_position.zip_map(&player_position, |a, b| a.min(b));
            max_position = max_position.zip_map(&player_position, |a, b| a.max(b));
        }

        // Reserve space for walls
        min_position -= Vector2::new(1, 1);
        max_position += Vector2::new(1, 1);

        if min_position.x < 0 {
            player_position.x = min_position.x.abs();
        }
        if min_position.y < 0 {
            player_position.y = min_position.y.abs();
        }

        let dimensions = min_position.abs() + max_position.abs() + Vector2::new(1, 1);
        let mut instance = Map::with_dimensions(dimensions);

        // The initial position of boxes are the box positions, and the final position
        // of boxes are the goal positions
        let mut initial_box_positions = HashSet::new();
        let mut final_box_positions = HashSet::new();

        let mut final_player_position = player_position;
        for action in &**actions {
            instance[final_player_position] = Tiles::Floor;
            final_player_position += &action.direction().into();
            if action.is_push() {
                // The player pushed the box when moving, which means there is a box at the
                // player's current location
                if !final_box_positions.contains(&final_player_position) {
                    final_box_positions.insert(final_player_position);
                    initial_box_positions.insert(final_player_position);
                }
                final_box_positions.remove(&final_player_position);
                final_box_positions.insert(final_player_position + &action.direction().into());
            }
        }
        instance[final_player_position] = Tiles::Floor;

        let box_positions = initial_box_positions;
        let goal_positions = final_box_positions;
        if box_positions.is_empty() {
            return Err(ParseMapError::NoBoxOrGoal);
        }

        instance[player_position].insert(Tiles::Player);
        for box_position in &box_positions {
            instance[*box_position].insert(Tiles::Box);
        }
        for goal_position in &goal_positions {
            instance[*goal_position].insert(Tiles::Goal);
        }

        instance.add_walls_around_floors();

        instance.player_position = player_position;
        instance.box_positions = box_positions;
        instance.goal_positions = goal_positions;

        // Verify solution
        let mut level = Level::from_map(instance.clone());
        for action in &**actions {
            level
                .do_move(action.direction())
                .map_err(|_| ParseMapError::InvalidActions)?;
        }

        Ok(instance)
    }
}

https://rust-lang.github.io/api-guidelines/interoperability.html#error-types-are-meaningful-and-well-behaved-c-good-err

https://doc.rust-lang.org/std/io/struct.BufReader.html

https://docs.rs/thiserror/latest/thiserror/

标准化

在关卡设计中, 有时会为了美观在原关卡基础上添加一些装饰性元素, 但这些装饰性的元素本质上并不会影响关卡的解法.
标准化的目的是移除这些与求解无关或冗余的元素.

理想情况下, 任何具有相同步数最优解的关卡都可以标准化为同一个关卡. 理论上, 可以先对关卡进行自动求解, 获得最优解决方案后, 再从解决方案构造关卡来得到标准化后的关卡.
然而, 对于 PSPACE-complete 的推箱子问题来说, 通过自动求解获得最优解决方案通常是耗时且困难的, 因此还需要一种不依赖于关卡解决方案的高效(多项式时间内得出结果)标准化方法. 尽管该方法得到的标准化结果并不完美.

关卡的标准化可以分为以下几个步骤:

将不可移动的箱子变为墙.

箱子可能默认就处于死锁状态, 可以将其视为墙体.
将无需使用的地板变为墙.

如果一个地板被三面墙包围, 属于死胡同, 可以将其视为墙体.
移除无法到达的墙.

部分墙无法与玩家产生交互, 因此移除这部分墙不影响关卡的解决方案.
统一外墙形式.

外墙有不同的包围类型, 如:
```
 ###
#@$.#
 ###

#####
#@$.#
#####
```
应该统一为其中一种类型, 通常使用下面的类型.
移除无法到达的箱子.

部分箱子无法与玩家产生交互, 因此移除这部分箱子不影响关卡的解决方案.
收紧地图尺寸.

地图中的元素被删除可能导致地图尺寸缩小.
对旋转和翻转标准化.

将经过不同旋转和翻转的关卡标准化为同一个关卡. 一个简单的方法是计算不同旋转和翻转后地图的哈希值，选择哈希值最小的版本.
玩家初始位置标准化. (注意: 可能移动玩家位置, 进而改变关卡的解决方案)

需要对先对玩家的位置进行标准化. 因为即使玩家位置不一样, 但都在同一个区域也可以转变为同一个关卡. 一个简单的玩家位置标准化方法是将玩家的位置设为玩家可达区域的位置中 Y 坐标最小, 其次 X 坐标最小的位置.

激进的标准化

激进的标准化可能改变关卡的解. 以最简单的关卡为例:

#####
#@$.#
#####

因为玩家开始的位置三面有墙, 位于死胡同, 只能向右移动. 得到结果:

#####
# @*#
#####

玩家左侧死胡同属于无用的区域, 使用墙体填充. 玩家右侧位于目标上的箱子处于死锁状态, 属于无用的箱子和目标, 使用墙体填充. 最后移除多余的墙体得到激进的标准化结果:

###
#@#
###

这是一个最简单的非标准关卡, 因为其没有箱子和目标, 解为空.

求解器(Solver)

顾名思义, 求解器是用于自动求解推箱子关卡的程序.

阅读本文前, 读者需要自行了解搜索算法的工作原理. 因为相比推箱子求解, 一般的寻路算法更适合读者理解搜索算法.

图(Graph)

以下面关卡为例:

######
# @$.#
######

该关卡存在三种状态, 分别为:

A:        B:        C:
######    ######    ######
# @$.#    #@ $.#    #  @*#
######    ######    ######

为了更直观地展示这些状态之间的转换关系, 可以用图的形式表示为:

graph TD
    A-->|l| B
    B-->|r| A
    A-->|R| C
    C-->|L| A

这是一个以状态(State)为节点(Vertex), 动作(Action)为边(Edge)的有向图(Directed graph).
其中 $A$ 为初始状态(Initial state, IS), $C$ 为目标状态(Goal state, GS), l 和 r 分别表示玩家向左和向右移动, R 和 L 分别表示玩家向右推动和向左拉动.

理论上, 状态 $C$ 还可以衍生出更多子状态, 但因为其是目标状态, 搜索算法无需继续搜索, 因此这里不再展开.

求解器的工作是进行空间状态搜索¹, 即首先根据初始状态生成推箱子关卡的图, 然后在这个图中寻找从初始状态到目标状态的路径. 以上图为例, 就是寻找从状态 $A$ 到状态 $C$ 的路径, 即 R.

寻路算法是在路径点组成的图中寻找一条从初始位置到目标位置的路径.
求解器则是在状态组成的图中寻找一条从初始状态到目标状态的路径, 即移动箱子的顺序.

下面将详细探讨如何利用搜索算法来找到这条路径.

搜索算法

广度优先搜索算法(Breadth-first search, BFS)².
A* 搜索算法³

A* 与 BFS 在最坏情况下的时间复杂度均为 $O (b^{d})$ . 但 A* 算法是一种最佳优先搜索(Best-first search)算法, 会优先探索最有希望的节点.
IDA* 搜索算法⁴

相比空间复杂度为 $O (b^{d})$ 的 A* 算法, IDA* 算法的空间复杂度为 $O (d)$ .
FESS 搜索算法⁵

A* 和 IDA* 算法只通过单个启发式函数值值来选择下一个探索的节点.
虽然可以通过计算出多个启发式函数值, 将它们融合为单个启发式函数值, 以同时利用多种启发式函数, 但由于多个启发式函数值被融合为了一个, 因此无法区分单个启发式函数值的变化趋势. FESS 算法则在这方面做出了改进. 该论文的第一作者 Yaron Shoham 还将该算法应用在了求解器 Festival⁶ 上, 并取得了极佳的效果⁷.

本文不会进一步探讨 FESS 算法, 感兴趣的读者可以阅读相关论文.

BSF/A*/IDA* 算法均可以用于搜索最短路径, 即最佳解决方案.
由于推箱子问题是PSPACE完全(PSPACE-complete)的, 使用 BSF 这种非启发式算法是难以搜索到解决方案的.
而 IDA* 算法则是基于 A* 算法的改进, 所以本文将描述如何创建一个基于 A* 搜索算法的求解器.

表示状态

状态只需要包含了玩家的位置和箱子的位置, 因为玩家和箱子是关卡中可移动对象. 保存它们的位置足以描述整个关卡的状态.
其他元素, 如墙壁/目标位置等是静态的，它们的位置不会随状态的改变而改变, 因此只需要从关卡的初始状态中获取它们的位置.

pub struct State {
    pub player_position: Vector2<i32>,
    pub box_positions: HashSet<Vector2<i32>>,
}

其中 box_positions 使用容器 HashSet 存储是因为箱子位置没有顺序关系, 且不会重复. 相较于常用的 Vec 容器, 它能更快的进行比较和查找.

实现从 Map 到 State 的转换:

impl From<Map> for State {
    fn from(map: Map) -> Self {
        Self {
            player_position: map.player_position(),
            box_positions: map.box_positions().clone(),
        }
    }
}

这样就可以将地图转为初始状态, 然后作为搜索起点开始搜索.

flowchart LR
    A{是否有\n未探索的状态} -->|是| B
    A -->|否| H[返回无解]
    B[取出优先级\n最高的未探索状态] --> C{是目标状态?}
    C -->|是| D[返回解决方案]
    C -->|否| E["生成其子状态(邻域)"]
    E --> F{是否已访问过?}
    F -->|是| E
    F -->|否| G[将子状态加入 heap]
    G --> A

创建一个新的结构体用于存储到状态的代价和启发式函数值:

pub struct Node {
    pub state: State,
    pub pushes: i32,
    pub moves: i32,
    priority: i32,
}

对于未探索的状态, 可以利用 BinaryHeap 容器来存储. 因为该容器能够高效地取出最大的元素.

通过重载 Node 的 Ord trait, 可以将状态通过优先级排序.

impl Ord for Node {
    fn cmp(&self, other: &Self) -> Ordering {
        self.priority.cmp(&other.priority).reverse()
    }
}

impl PartialOrd for Node {
    fn partial_cmp(&self, other: &Self) -> Option<Ordering> {
        Some(self.cmp(other))
    }
}

其中 priority 的值是根据搜索策略而计算的.

值得注意的是, Rust 中的 BinaryHeap 的实现方式是最大栈(max-heap), 因此 BinaryHeap::pop 函数返回的是容器中最大的元素. 而优先级的值越小表示优先级越高, 因此比较后还需要调用 Ordering::reverse 函数.
这样该便可以从容器中取出优先级最高(即最小)的状态.

标准化玩家位置

玩家的移动会产生大量新的状态, 然而许多状态仅仅是玩家在固定区域内反复移动而未对箱子位置产生任何影响, 这些状态对于求解问题并无实质性贡献. 例如:

#####
#   ###
#  @$.#
#######

尽管玩家可以在箱子的左侧区域内活动, 但只有当玩家向右推动箱子时, 才能对求解做出贡献.

在移动数优先的搜索策略里, 生成仅移动的状态能确保角色以最短路径移动. 但这也可以通过更高效的最优寻路算法来实现.

因此, 如果玩家只是在一个区域内移动而不推动箱子, 对于推箱子求解是没有意义的. 为了减少这类无用状态的产生, 可以在状态中存储玩家可移动的区域和箱子的位置.

存储玩家可移动区域的一个简单且高效的实现方法是将玩家的位置标准化.
即将玩家移动到一个特殊的位置, 比如设置到可移动区域中最左其次最上的位置. 这样在箱子布局一样的情况下, 玩家标准化位置相同就意味着玩家可达区域相同.

pub fn normalized_area(area: &HashSet<Vector2<i32>>) -> Option<Vector2<i32>> {
    area.iter()
        .min_by(|a, b| a.y.cmp(&b.y).then_with(|| a.x.cmp(&b.x)))
        .copied()
}

生成邻域

从初始状态开始探索其相邻的节点, 即邻域⁸.

通过下面函数来生成当前状态的派生状态, 即相邻的状态:

impl State {
    pub fn successors(&self, solver: &Solver) -> Vec<State> {
        // ... SKIP ...
    }
}

因为只有推动箱子的状态才有价值, 该函数会尝试在当前状态的基础上生成产生推动而不只是产生移动的状态.

搜索

一个只能判断是否有解决方案的简单实现如下:

impl Solver {
    pub fn a_star_search(&self, map: &Map) -> Result<(), SearchError> {
        let mut heap = BinaryHeap::new();
        let mut visited = HashSet::new();

        let state: State = map.clone().into();
        heap.push(Node::new(state, 0, self));

        while let Some(Node { state, cost, .. }) = heap.pop() {
            if state.is_solved(self) {
                return Ok(());
            }
            for successor in state.successors(self) {
                if !visited.insert(successor.normalized_hash(map)) {
                    continue;
                }
                heap.push(Node::new(successor, cost + 1, self));
            }
        }
        Err(SearchError::NoSolution)
    }
    // ... SKIP ...
}

转置表(Transposition table)

复杂推箱子关卡的图可能存在环(Loop), 这意味着:

需要记录已探索过的节点, 避免进入环中导致死循环.
推箱子关卡的状态可以用图表示, 却无法用树(Tree)表示.

已被探索的节点通常会被存储在一个闭集(Closed set)中, 为了通俗易懂, 使用变量名 visited 表示这个闭集.
为了节省内存, visited 中只需要存储已访问状态的哈希值, 因为这些状态将不会再被使用.

复杂推箱子关卡的图非常大, 难以提前生成并存储在内存中. 因此可以在搜索的过程中逐步拓展图.

https://en.wikipedia.org/wiki/State_space_search

https://en.wikipedia.org/wiki/Breadth-first_search

https://en.wikipedia.org/wiki/A*_search_algorithm

⁴

https://en.wikipedia.org/wiki/Iterative_deepening_A*

⁵

Y. Shoham and J. Schaeffer, "The FESS Algorithm: A Feature Based Approach to Single-Agent Search," 2020 IEEE Conference on Games (CoG), Osaka, Japan, 2020, pp. 96-103, doi: 10.1109/CoG47356.2020.9231929

⁶

https://festival-solver.site/

⁷

http://sokobano.de/wiki/index.php?title=Solver_Statistics

⁸

https://en.wikipedia.org/wiki/Neighbourhood_(graph_theory)

搜索策略

什么是最短路径?

在常见的寻路算法中, 最短可能是指距离最短, 也可能是指时间最短.
在推箱子中也是如此, 既有移动数最优解决方案, 也有推动数最优解决方案.

策略

推箱子求解器通常有以下策略:

Fast: A* 算法可以用于搜索最短路径, 但不一定只能搜索最短路径. 通过提高启发式函数的权重可以提高搜索到任何解决方案的效率, 即速度.
OptimalPush: 搜索推动数最少的解决方案.
OptimalMove: 搜索移动数最少的解决方案.
搜索推动数最少其次移动数最少的解决方案.
搜索移动数最少其次推动数最少的解决方案.

表示

pub enum Strategy {
    /// Search for any solution as quickly as possible
    Fast,

    /// Find the push optimal solution
    OptimalPush,

    /// Find the move optimal solution
    OptimalMove,
}

启发式函数(Heuristic function)

启发式函数用于指导搜索算法的搜索方向.

A* 算法的核心是估价函数 $f$ , $f (n) = g (n) + h (n)$ . 其中:

$n$ 是某个状态.
$g (n)$ 为从初始状态到 $n$ 状态的实际代价.
$h (n)$ 为从 $n$ 状态到目标状态的代价的估计代价.

搜索最短路径就是指搜索总代价(即 $f$ 的函数值)最小的路径. 以推箱子为例:

代价可能指玩家移动数, 也可能指箱子推动数, 这取决于求解器的搜索策略. 因此针对不同的搜索策略, 于代价相关的函数 $g$ 和 $h$ 的实现不同.
路径就是解决方案.

该算法总是能搜索到最优路径, 前提是启发式函数 $h$ 满足容许性(Admissible)¹.

容许性(Admissible)

启发式函数满足容许性, 才能确保结果是最优的. 若函数 $h$ 满足以下条件则满足容许性:

$\forall n, h (n) \leq h^{*} (n)$

其中 $h^{*} (n)$ 是从 $n$ 状态到目标状态的实际代价.

对于最优路径上的任意状态 $m$ , 到目标状态的实际代价总是为 $h^{*} (m)$ . 若 $h (n) > h^{*} (n)$ , 在搜索 $g$ 函数值相同的节点时, 一定会跳过最优路径, 进而返回非最优路径.
函数 $h$ 不满足容许性也可能返回最优路径, 因为 $h (n) > h^{*} (n)$ 不一定恒成立.

设计的方向

假设 $h (n) = 0$ , 此时函数 $h$ 满足容许性, 但不再能启发搜索方向, 该情况下的 A* 算法也被称之为相同代价搜索(Uniform-cost search, UCS), 下一个搜索节点的优先级为 $f (n) = g (n)$ , 行为与 BFS 类似. 虽然可以得到最优解, 但无法得到 "启发式" 带来的任何的优化.
理想状态下 $h (n) = h^{*} (n)$ , 但这不可能. 因此函数 $h$ 应该在满足容许性的前提下, 尽可能的接近 $h^{*} (n)$ .

对于网格上的寻路算法, 一种启发式函数的实现是计算当前位置和目标位置之间的曼哈顿距离. 相比之下, 推箱子的启发式函数实现并不那么显而易见.
理想状态下, 函数 $h$ 对于任意关卡的任意解决方案 $n_{1}, n_{2}, ..., n_{k}$ , 应满足以下条件:

$h (n_{i}) > h (n_{i + 1})$
$h (n_{1}) = 0$
$h (n_{k}) = h^{*} (n_{k})$

预计算

启发式函数计算的适合通常会假设地图上只有一个箱子, 因为这样计算出的结果与箱子的位置无关. 在搜索状态的时候箱子的位置会不断发生改变, 但是启发式函数的值不变.
因此可以提前计启发式函数的值, 供后续搜索时使用.

下界(Lower bounds)

根据搜索策略有两种下界:

推动下界: 将箱子推动到任何目标的最少推动数.
移动下界: 将箱子推动到任何目标的最少移动数.

其中推动下界可以用于搜索最优移动数解决方案, 反之则不行. 因为推动下界一定小于移动下界.

最简单的推动下界计算方法是计算每个箱子到最近目标的曼哈顿距离². 曼哈顿距离也是网格中寻路常用的启发式函数的计算方法.

TODO: 使用二维数组而非 HashMap 来存储下界.

fn manhattan_distance(a: Vector2<i32>, b: Vector2<i32>) -> u32 {
    (a.x - b.x).abs() + (a.y - b.y).abs()
}

let mut lower_bounds = HashMap::new();
for x in 1..self.map.dimensions().x - 1 {
    for y in 1..self.map.dimensions().y - 1 {
        let position = Vector2::new(x, y);
        if self.level[position].intersects(Tiles::Goal) {
            lower_bounds.insert(position, 0);
            continue;
        }
        if !self.map[position].intersects(Tiles::Floor) {
            continue;
        }
        let lower_bound = self
            .map
            .goal_positions()
            .iter()
            .map(|box_position| manhattan_distance(*box_position, &position))
            .min()
            .unwrap(); // 地图上的目标不可能为空 => 迭代器不可能为空 => `Iterator::min` 不可能返回 `None`
        lower_bounds.insert(position, lower_bound);
    }
}
lower_bounds

上面算法的时间复杂度为 $O (n * m * k)$ , 其中 $n$ , $m$ 为地图尺寸, $k$ 为目标数量.
其中函数 manhattan_distance 的时间复杂度为 $O (1)$ .

该方法的有点是计算十分快速, 缺点是其忽视了墙体对玩家和箱子的阻碍, 可能严重低估了推动下界.

实现

启发式函数需要计算当前状态到目标状态的下界.
所有箱子所在位置的下界之和.

impl State {
    fn calculate_lower_bound(&self, solver: &Solver) -> usize {
        self.box_positions
            .iter()
            .map(|box_position| solver.lower_bounds()[&box_position])
            .sum()
    }
    // ... SKIP ...
}

https://en.wikipedia.org/wiki/Admissible_heuristic

https://simple.wikipedia.org/wiki/Manhattan_distance

优化

在计算复杂性理论中, 推箱子属于 PSPACE-complete 问题, 是 PSPACE 中最难的一类问题. 推箱子的地图尺寸和箱子数量没有限制. 这类问题目前只能在超多项式时间(superpoly-nomial)内解决.
因此没有任何优化的暴力搜索只能解决非常简单(地图尺寸小, 箱子数量少)的关卡, 如果希望解决更复杂的关卡则需要对求解器进行优化.

本文所描述的求解器将使用以下优化手段:

启发式搜索(Heuristic search): 使用启发式搜索算法, 通过引入启发式函数来指导搜索方向.
剪枝(Pruning): 借助死锁检测, 我们能够有效地剪去部分不可能导致解的情况, 减少搜索空间.
记忆化搜索(Memoization): 防止搜索过程中重复搜索相同节点, 或陷入图里的环.
预处理(Preprocessing): 预计算下界, 在之后的搜索过程中可以直接取用, 避免反复计算下界.

隧道(Tunnels)

一般情况下, 箱子的移动会产生一个新的状态, 该状态可能包含其他箱子移动所生成的子状态, 这是因为箱子之间可能存在相互影响.
然而, 在部分关卡中, 存在一种被称为隧道的结构, 它可以将位于隧道内的箱子与隧道外的箱子隔绝, 使它们之间互不影响.

如下图所示, 其中蓝色矩形描边区域为隧道:

当上方的箱子位于隧道时, 两个箱子之间不会产生影响. 此时推动隧道内的箱子被视作无影响力推动(No influence pushes).

在有 $n$ 个箱子的关卡中, 每一个状态最多有 $n$ 个子状态. 但如是无影响力推动, 则无需产生对应的子状态, 应该继续推动箱子, 直到产生有影响力的推动(即该箱子离开隧道), 并产生 1 个子状态.

停放

将箱子推入隧道内的推动是有影响力的, 这意味这将该箱子停放到隧道内, 并为玩家和其他箱子的移动腾出空间.

单个隧道内最多能停放一个箱子. 因为隧道中不存在目标, 停放多个箱子会产生畜栏死锁, 进而导致关卡无解.

隧道内停放箱子的最佳位置是隧道入口, 此处的隧道入口指的是距离箱子最近的隧道口.
因为如果停放在隧道的其他位置, 玩家还需要重新返回隧道入口才能离开封闭的隧道, 这意味着玩家需要原路返回, 增加了不必要的移动步数.

识别

若推动后产生了如下的模式(包括旋转和镜像), 则表示箱子已经被推入隧道, 属于无效推动. 此时应该继续推动箱子, 直到箱子离开隧道, 产生具有有效推动的子状态.

隧道模式 1 隧道模式 2

下面是计算隧道的实现, 通过遍历地图, 识别符合 2 种隧道模式(包括镜像和旋转)的位置并进行标记. 计算结果可以被缓存, 以便在后续求解过程中快速判断隧道.

impl Solver {
    fn calculate_tunnels(&self) -> HashSet<(Vector2<i32>, Direction)> {
        let mut tunnels = HashSet::new();
        for x in 1..self.map.dimensions().x - 1 {
            for y in 1..self.map.dimensions().y - 1 {
                let box_position = Vector2::new(x, y);
                if !self.map[box_position].intersects(Tiles::Floor) {
                    continue;
                }

                for (up, right, down, left) in [
                    Direction::Up,
                    Direction::Right,
                    Direction::Down,
                    Direction::Left,
                ]
                .into_iter()
                .circular_tuple_windows()
                {
                    let player_position = box_position + &down.into();

                    //  .
                    // #$#
                    // #@#
                    if self.map[player_position + &left.into()].intersects(Tiles::Wall)
                        && self.map[player_position + &right.into()].intersects(Tiles::Wall)
                        && self.map[box_position + &left.into()].intersects(Tiles::Wall)
                        && self.map[box_position + &right.into()].intersects(Tiles::Wall)
                        && self.map[box_position].intersects(Tiles::Floor)
                        && self
                            .lower_bounds()
                            .contains_key(&(box_position + &up.into()))
                        && !self.map[box_position].intersects(Tiles::Goal)
                    {
                        tunnels.insert((player_position, up));
                    }

                    //  .      .
                    // #$_ or _$#
                    // #@#    #@#
                    if self.map[player_position + &left.into()].intersects(Tiles::Wall)
                        && self.map[player_position + &right.into()].intersects(Tiles::Wall)
                        && (self.map[box_position + &right.into()].intersects(Tiles::Wall)
                            && self.map[box_position + &left.into()].intersects(Tiles::Floor)
                            || self.map[box_position + &right.into()].intersects(Tiles::Floor)
                                && self.map[box_position + &left.into()].intersects(Tiles::Wall))
                        && self.map[box_position].intersects(Tiles::Floor)
                        && self
                            .lower_bounds()
                            .contains_key(&(box_position + &up.into()))
                        && !self.map[box_position].intersects(Tiles::Goal)
                    {
                        tunnels.insert((player_position, up));
                    }
                }
            }
        }
        tunnels
    }

    // ... SKIP...
}

参考

http://sokobano.de/wiki/index.php?title=Solver#Tunnels.

死锁(Deadlock)

本文中的死锁示例图片来源于 http://sokobano.de/wiki.

箱子在被推动到某个位置后, 再也无法被推动. 这种情况被称之为死锁. 如果此时被死锁的箱子不在目标上, 意味着该箱子后续无法被推动至目标上, 导致无法通关.

为什么要检测死锁

优化求解器: 可以在搜索时进行可行性剪枝.

若被死锁的箱子不在目标上, 那么该状态及其衍生状态一定无解.
部分死锁存在特定的模式, 可以通过较小的代价进行检测, 从而使求解器跳过无意义的搜索.
提升玩家体验: 可以警告或防止玩家产生死锁状态.

比如在显示箱子可达位置时不显示会产生死锁的箱子位置.

静态死锁

检测时机: 因为该类型的死锁只与关卡的地形有关, 因此可以在最开始进行计算, 之后在箱子被死锁时进行更新. 被死锁的箱子可以被当成墙体, 进而导致关卡地形发生变化.

Static deadlock - Sokoban Wiki

以上图为例, 暗色格子属于静态死锁区域. 若箱子被推动到这些区域则会导致该箱子永远无法再被推到目标上.

这种死锁与箱子和玩家的位置无关, 可以在只知道关卡地形和目标位置的情况下进行计算. 但关卡地形也可能发生变化:

Static deadlock - Sokoban Wiki

以上图为例, 箱子向右被推入死角, 导致冻结死锁. 此时该箱子无法再被移动, 可以视作墙体, 进而导致关卡地形发生变化, 需要重新计算静态死锁区域.

这类地形变化只会增加墙体, 导致静态死锁区域增加. 因此即使不在地形变化时重新计算也不会导致误报, 但可能导致静态死锁检测不全面.

pub fn is_static_deadlock(
    map: &Map,
    box_position: Vector2<i32>,
    box_positions: &HashSet<Vector2<i32>>,
    visited: &mut HashSet<Vector2<i32>>,
) -> bool {
    debug_assert!(box_positions.contains(&box_position));

    if !visited.insert(box_position) {
        return true;
    }

    for direction in [
        Direction::Up,
        Direction::Right,
        Direction::Down,
        Direction::Left,
    ]
    .windows(3)
    {
        let neighbors = [
            box_position + &direction[0].into(),
            box_position + &direction[1].into(),
            box_position + &direction[3].into(),
        ];
        for neighbor in &neighbors {
            if map[*neighbor].intersects(Tiles::Wall) {
                continue;
            }
            if box_positions.contains(neighbor)
                && is_static_deadlock(map, *neighbor, box_positions, visited)
            {
                continue;
            }
            return false;
        }
    }
    true
}

二分死锁(Bipartite deadlocks)

静态死锁检测的是指定箱子能否被推动至目标上, 而二分死锁检测的是箱子能否被推动至指定目标上.

Bipartite deadlocks - Sokoban Wiki

以上图为例, 箱子被推动至右侧, 但不属于静态死锁区域, 因为箱子看似可以继续向下推动至目标. 但将导致没有箱子能被推动至位于 $(3, 3)$ 的目标.

冻结死锁(Freeze deadlocks)

检测时机: 箱子推动后.

若一个箱子在水平和垂直方向均不可能移动, 则出现冻结死锁.

能遮挡箱子的元素有两个:

墙体.
其他箱子: 需递归的判断该箱子是否被死锁.

在递归的检查其他箱子是否死锁时会产生循环检查, 即已检查过的节点会被重复检查, 从而形成死循环.

为避免循环检查, 可以将已检查的箱子视为被死锁的, 原因如下:

如下 XSB 关卡所示, 有箱子 A, B, C. 其中 B 的左侧和下方是空地:

 A
_BC
 _

此时需要判断箱子 B 是否处于冻结死锁.

假设 B 被死锁时 A 也被死锁, 则 A 是否被死锁, 取决于 B 是否能在水平方向上移动, 即 C 是否被死锁. 需要继续检测 C 是否被死锁.
假设 B 被死锁时 C 也被死锁, 则 C 是否被死锁, 取决于 B 是否能在垂直方向上移动, 即 A 是否被死锁. 需要继续检测 A 是否被死锁.

如果在 B 被假设死锁时, A, C 均被死锁, 则 B 一定被死锁. 因为 A 被死锁意味着 B 不能在垂直方向上移动, 而 C 被死锁意味着 B 不能在水平方向上移动, 因此 B 处于冻结死锁状态.

综上所述, 将已被检测的箱子视为被死锁可以确保程序的行为正确.

如下图所示, 冻结死锁可能产生连锁反应, 即单个箱子被死锁后, 可能导致相连的箱子也被死锁.

Freeze deadlock - Sokoban Wiki

pub fn is_freeze_deadlock(
    map: &Map,
    box_position: Vector2<i32>,
    box_positions: &HashSet<Vector2<i32>>,
    visited: &mut HashSet<Vector2<i32>>,
) -> bool {
    debug_assert!(box_positions.contains(&box_position));

    if !visited.insert(box_position) {
        return true;
    }

    for direction in [
        Direction::Up,
        Direction::Down,
        Direction::Left,
        Direction::Right,
    ]
    .chunks(2)
    {
        let neighbors = [
            box_position + &direction[0].into(),
            box_position + &direction[1].into(),
        ];

        // Check if any immovable walls on the axis.
        if map[neighbors[0]].intersects(Tiles::Wall) || map[neighbors[1]].intersects(Tiles::Wall) {
            continue;
        }

        // Check if any immovable boxes on the axis.
        if (box_positions.contains(&neighbors[0])
            && is_freeze_deadlock(map, neighbors[0], box_positions, visited))
            || (box_positions.contains(&neighbors[1])
                && is_freeze_deadlock(map, neighbors[1], box_positions, visited))
        {
            continue;
        }

        return false;
    }
    true
}

资源

http://sokobano.de/wiki/: 推箱子 Wiki, 德国.
https://sourceforge.net/projects/sokobanyasc/ 推箱子软件 SokobanYASC.
https://www.sokoban-online.de/: 推箱子软件 JSoko.
https://ygp.orgfree.com/ 推箱子软件 YSokoban.
https://sokoban.cn/: 推箱子平台, 魔方吧推箱子比赛, 中国.
https://sokoban.jp/ 推箱子官网, 日本.

术语表

中文	英文
求解器	solver
解决方案/解	solution
动作	action
容器¹	collection

collection 被翻译为 "容器", 延用了 C++ 中的叫法. 不译为 "集合" 是为了防止与集合 "set" 混淆.

现代推箱子教程